A generic matrix. More...

#include <matrix.h>

Public Types
using	value_type = typename std::array< Vector< M, T >, N >::value_type

using	size_type = typename std::array< Vector< M, T >, N >::size_type

using	iterator = typename std::array< Vector< M, T >, N >::iterator

using	const_iterator = typename std::array< Vector< M, T >, N >::const_iterator

Public Member Functions
constexpr	Matrix ()=default
	Construct a new Matrix object. More...

template<typename... TArgs>
	Matrix (TArgs const(&&... rows)[M])
	Construct a new Matrix object from a number of NxM values. More...

template<std::size_t Nn, std::size_t Mm, class U >
	Matrix (const Matrix< Nn, Mm, U > &m)
	Construct a new Matrix from an existing Matrix of a different type. More...

	Matrix (const std::array< Vector< M, T >, N > &a)
	Construct a new Matrix object from an std::array of Vectors. More...

template<typename U = T>
	Matrix (const std::array< Vector< M, U >, N > &a)
	Construct a new Matrix object from an std::array of Vectors of a different type. More...

template<typename U = T, std::enable_if_t< std::is_arithmetic< U >::value, int > = 0>
	Matrix (const std::array< std::array< U, M >, N > &a)
	Construct a new Matrix object from an std::array of std::arrays. possibly of a different type. More...

template<typename U = T, std::enable_if_t< std::is_arithmetic< U >::value, int > = 0>
	Matrix (const U &value)
	Construct a new Matrix object from a single value possibly of a different type. More...

	~Matrix ()=default
	Destroy the Matrix object.

	Matrix (const Matrix &other)=default
	Copy construct a new Matrix object. More...

	Matrix (Matrix &&other) noexcept=default
	Move construct a new Matrix object. More...

Matrix &	operator= (const Matrix &other)=default
	Copy assignment operator. More...

Matrix &	operator= (Matrix &&other) noexcept=default
	Move assignment operator. More...

Vector< M, T > &	operator[] (size_type idx) noexcept
	access a row within the matrix More...

const Vector< M, T > &	operator[] (size_type idx) const noexcept
	const access a row within the matrix More...

Vector< M, T > &	at (size_type idx)
	access a row within the matrix More...

const Vector< M, T > &	at (size_type idx) const
	const access a row within the matrix More...

constexpr std::array< size_type, 2 >	size () const noexcept
	returns the matrix dimensions as an array of size 2 More...

constexpr size_type	n_rows () const noexcept
	returns the number of rows More...

constexpr size_type	n_cols () const noexcept
	returns the number of columns More...

iterator	begin () noexcept
	returns an iterator starting at the first row More...

const_iterator	begin () const noexcept
	returns a const iterator starting at the first row More...

iterator	end () noexcept
	returns a iterator starting at one after the last row More...

const_iterator	end () const noexcept
	returns a const iterator starting at one after the last row More...

Vector< M, T >	row (const size_type &idx) const
	get a matrix row as a vector More...

Vector< N, T >	col (const size_type &idx) const
	get a matrix column as a vector More...

T	min () const
	get the min value of the matrix More...

T	max () const
	get the max value of the matrix More...

T	sum () const
	sum up all the elements of the matrix More...

template<typename U = T>
U	mean () const
	mean of all the elements of the matrix More...

auto	diag () const
	returns the diagonal of the matrix as a vector More...

T	det () const
	calculates the determinant of the matrix More...

void	transpose ()
	transposes this Matrix object More...

Matrix< M, N, T >	transposed () const
	creates and returns a transposed Matrix object More...

template<typename U = void, std::size_t N2, std::size_t M2, typename T2 >
std::conditional_t< std::is_same< U, void >::value, Matrix< N, M2, T >, Matrix< N, M2, U > >	dot (const Matrix< N2, M2, T2 > &rhs) const
	dot product of two matrices More...

template<typename U = void, std::size_t N2, typename T2 >
std::conditional_t< std::is_same< U, void >::value, Vector< N, T >, Vector< N, U > >	dot (const Vector< N2, T2 > &rhs) const
	dot product of a matrix and a vector More...

template<class U = T>
U	std () const
	calculates the standard deviation More...

template<typename U = T>
bool	operator== (const Matrix< N, M, U > &rhs) const
	equality operator More...

template<typename U = T>
bool	operator!= (const Matrix< N, M, U > &rhs) const
	unequality operator More...

template<typename U = T>
Matrix< N, M, T > &	operator+= (const Matrix< N, M, U > &rhs)
	plus equal operator More...

template<typename U = T>
Matrix< N, M, T > &	operator-= (const Matrix< N, M, U > &rhs)
	minus equal operator More...

template<typename U = T>
Matrix< N, M, T > &	operator*= (const Matrix< N, M, U > &rhs)
	multiplication equal operator More...

template<typename U = T>
Matrix< N, M, T > &	operator/= (const Matrix< N, M, U > &rhs)
	divison equal operator More...

template<class TScalar >
std::enable_if_t< std::is_arithmetic< TScalar >::value, Matrix< N, M, T > & >	operator+= (const TScalar &scalar)
	add a scalar to this matrix More...

template<class TScalar >
std::enable_if_t< std::is_arithmetic< TScalar >::value, Matrix< N, M, T > & >	operator-= (const TScalar &scalar)
	subtract a scalar from every element of this matrix More...

template<class TScalar >
std::enable_if_t< std::is_arithmetic< TScalar >::value, Matrix< N, M, T > & >	operator*= (const TScalar &scalar)
	multiply a scalar with this matrix More...

template<class TScalar >
std::enable_if_t< std::is_arithmetic< TScalar >::value, Matrix< N, M, T > & >	operator/= (const TScalar &scalar)
	divide every element of this matrix by a scalar More...

Protected Attributes
std::array< Vector< M, T >, N >	data_

Friends
template<std::size_t Nn, std::size_t Mm, class U >
std::ostream &	operator<< (std::ostream &os, const Matrix< Nn, Mm, U > &m)
	print matrix values More...

Detailed Description

template<std::size_t N, std::size_t M, typename T>
class mu::Matrix< N, M, T >

A generic matrix.

Can be instantiated with an arithmetic type as defined by the standard library.

implementation-defined extended integer types, including any signed, unsigned, and cv-qualified variants. (bool, char, int, long ...)
implementation-defined extended floating-point types including any cv-qualified variants. (float, double, long double)

Template Parameters

N	first matrix dimension (rows)
M	second matrix dimension (columns)
T	the type of the values inside the matrix

forward declaration of the Matrix class

Template Parameters

X
Y
Z

Constructor & Destructor Documentation

◆ Matrix() [1/9]

template<std::size_t N, std::size_t M, typename T>

constexpr mu::Matrix< N, M, T >::Matrix ( )

default

Construct a new Matrix object.

Example: mu::Matrix<2, 2, int> a;

Here is the caller graph for this function:

◆ Matrix() [2/9]

template<std::size_t N, std::size_t M, typename T>

template<typename... TArgs>

mu::Matrix< N, M, T >::Matrix ( TArgs const (&&... rows)[M] )

inline

Construct a new Matrix object from a number of NxM values.

the number of values in every dimension must match the static size of this Matrix.

Example: // direct initialization
mu::Matrix<2, 3, int> a{{2, 3, 4}, {5, 6, 7}};
// list initialization
mu::Matrix<2, 3, int> b = {{2, 3, 4}, {5, 6, 7}};

Template Parameters

TArgs

Parameters

rows

◆ Matrix() [3/9]

template<std::size_t N, std::size_t M, typename T>

template<std::size_t Nn, std::size_t Mm, class U >

mu::Matrix< N, M, T >::Matrix ( const Matrix< Nn, Mm, U > & m )

inline

Construct a new Matrix from an existing Matrix of a different type.

implicit narrowing may be applied
it is checked that the Matrix sizes are the same
forwards intialization to Vector for every row

Example: mu::Matrix<2, 2, float> a = {{1.5F, 2.5F}, {3.5F, 4.5F}};
mu::Matrix<2, 2, int> b = {a};

Template Parameters

Nn
Mm
U

Parameters

m

Here is the call graph for this function:

◆ Matrix() [4/9]

template<std::size_t N, std::size_t M, typename T>

mu::Matrix< N, M, T >::Matrix ( const std::array< Vector< M, T >, N > & a )

inline

Construct a new Matrix object from an std::array of Vectors.

Example: std::array<mu::Vector<2, int>, 3> arr;
arr[0] = {3, 4};
arr[1] = {5, 6};
arr[2] = {7, 8};
// direct initialization
mu::Matrix<3, 2, int> a{arr};
// copy initialization
mu::Matrix<3, 2, int> b = arr;
// list initialization
mu::Matrix<3, 2, int> c = {arr};

Parameters

a

◆ Matrix() [5/9]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

mu::Matrix< N, M, T >::Matrix ( const std::array< Vector< M, U >, N > & a )

inline

Construct a new Matrix object from an std::array of Vectors of a different type.

implicit narrowing may be applied
forwards intialization to Vector for every row

Example: std::array<mu::Vector<2, float>, 3> arr;
arr[0] = {3.5F, 4.5F};
arr[1] = {5.5F, 6.5F};
arr[2] = {7.5F, 8.5F};
// direct initialization
mu::Matrix<3, 2, int> a{arr};
// copy initialization
mu::Matrix<3, 2, int> b = arr;
// list initialization
mu::Matrix<3, 2, int> c = {arr};

Template Parameters

U

Parameters

a

Here is the call graph for this function:

◆ Matrix() [6/9]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T, std::enable_if_t< std::is_arithmetic< U >::value, int > = 0>

mu::Matrix< N, M, T >::Matrix ( const std::array< std::array< U, M >, N > & a )

inline

Construct a new Matrix object from an std::array of std::arrays. possibly of a different type.

implicit narrowing may be applied
forwards intialization to Vector for every row

Example: std::array<std::array<int, 2>, 3> arr;
arr[0] = {3, 4};
arr[1] = {5, 6};
arr[2] = {7, 8};
// direct initialization
mu::Matrix<3, 2, int> a{arr};
// copy initialization
mu::Matrix<3, 2, int> b = arr;
// list initialization
mu::Matrix<3, 2, int> c = {arr};

Template Parameters

U

Parameters

a

Here is the call graph for this function:

◆ Matrix() [7/9]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T, std::enable_if_t< std::is_arithmetic< U >::value, int > = 0>

mu::Matrix< N, M, T >::Matrix ( const U & value )

inline

Construct a new Matrix object from a single value possibly of a different type.

all the values inside the vector will be set to this value
implicit narrowing may be applied
forwards intialization to Vector for every row

Example: // direct initialization
mu::Matrix<3, 3, int> a{5};
// copy initialization
mu::Matrix<3, 3, int> b = 5;
// list initialization
mu::Matrix<3, 3, int> c = {5};

Template Parameters

U

Parameters

value

Here is the call graph for this function:

◆ Matrix() [8/9]

template<std::size_t N, std::size_t M, typename T>

mu::Matrix< N, M, T >::Matrix ( const Matrix< N, M, T > & other )

default

Copy construct a new Matrix object.

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Matrix<2, 2, int> b{a};

Parameters

other

◆ Matrix() [9/9]

template<std::size_t N, std::size_t M, typename T>

mu::Matrix< N, M, T >::Matrix ( Matrix< N, M, T > && other )

defaultnoexcept

Move construct a new Matrix object.

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Matrix<2, 2, int> b{std::move(a)};

Parameters

other

Member Function Documentation

◆ at() [1/2]

template<std::size_t N, std::size_t M, typename T>

Vector<M, T>& mu::Matrix< N, M, T >::at ( size_type idx )

inline

access a row within the matrix

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Vector<2, int> b = a.at(0); // [ 1, 2 ]
int a21 = a.at(1).at(0); // 3

Exceptions

out of range

Parameters

idx

Returns: T&

◆ at() [2/2]

template<std::size_t N, std::size_t M, typename T>

const Vector<M, T>& mu::Matrix< N, M, T >::at ( size_type idx ) const

inline

const access a row within the matrix

Example: const mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Vector<2, int> b = a.at(0); // [ 1, 2 ]
int a21 = a.at(1).at(0); // 3

Exceptions

out of range

Parameters

idx

Returns: const T&

◆ begin() [1/2]

template<std::size_t N, std::size_t M, typename T>

iterator mu::Matrix< N, M, T >::begin ( )

inlinenoexcept

returns an iterator starting at the first row

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
mu::Vector<3, int> first = *a.begin(); // [ 1, 2, 4 ]

Returns: iterator

Here is the caller graph for this function:

◆ begin() [2/2]

template<std::size_t N, std::size_t M, typename T>

const_iterator mu::Matrix< N, M, T >::begin ( ) const

inlinenoexcept

returns a const iterator starting at the first row

Example: const mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
mu::Vector<3, int> first = *a.begin(); // [ 1, 2, 4 ]

Returns: const_iterator

◆ col()

template<std::size_t N, std::size_t M, typename T>

Vector<N, T> mu::Matrix< N, M, T >::col ( const size_type & idx ) const

inline

get a matrix column as a vector

an invalid index that exceeds the matrix dimension causes a runtime error

Example

Parameters

idx

Returns: Vector<N, T>

◆ det()

template<std::size_t N, std::size_t M, typename T>

T mu::Matrix< N, M, T >::det ( ) const

inline

calculates the determinant of the matrix

matrix must be symmetrical with N == M

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
int det = a.det(); // -2

Returns: T

Here is the caller graph for this function:

◆ diag()

template<std::size_t N, std::size_t M, typename T>

auto mu::Matrix< N, M, T >::diag ( ) const

inline

returns the diagonal of the matrix as a vector

the vector is of the size of the smallest matrix dimension. either N or M

return type specified as "auto" because otherwise doc does not generate correctly. otherwise would be:

std::conditional_t < N<M, Vector<N, T>, Vector<M, T>>

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Vector<2, int> diag = a.diag(); // [ 1, 4 ]

Returns: Vector<N,T> or Vector<M,T>

Here is the caller graph for this function:

◆ dot() [1/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = void, std::size_t N2, std::size_t M2, typename T2 >

std::conditional_t<std::is_same<U, void>::value, Matrix<N, M2, T>, Matrix<N, M2, U> > mu::Matrix< N, M, T >::dot ( const Matrix< N2, M2, T2 > & rhs ) const

inline

dot product of two matrices

For a Matrix \( A \) of size \( M \times N \) and a Matrix \( B \) of size \( N \times P \) the result is a Matrix \( C \) of size \( M \times P \),

\( C = A \cdot B \) with

\( c_{ij} = A_{i1} B_{1j} + A_{i2} B_{2j} + ... + A_{iN} B_{Nj} = \sum_{k=1}^{N} A_{ik} B_{kj} \)

Second Matrix dimension (N) of first Matrix must be equal to the first Matrix dimension of the second Matrix (N)

For two objects of the same type, specifying the return type is optional. It will be of the type of the two objects by default.

For two objects of different types, specifying the return type is required.

return value is a Matrix of the size of the first Matrix's first dimension (M) and the second Matrix's second dimension (P) containing the type of the two objects or else of the explicitly stated type

https://en.wikipedia.org/wiki/Matrix_multiplication#Definition

Example: // same types
mu::Matrix<2, 3, int> a{{1, 2, 3}, {4, 5, 6}};
mu::Matrix<3, 2, int> b{{3, 4}, {5, 6}, {7, 8}};
mu::Matrix<2, 2, int> res1 = a.dot(b); // [ [ 34, 40 ], [ 79, 94 ] ]
// different types (must specify internal precision)
mu::Matrix<2, 3, float> c{{1.5F, 2.5F, 3.5F}, {4.5F, 5.5F, 6.5F}};
mu::Matrix<3, 2, int> d{{3, 4}, {5, 6}, {7, 8}};
mu::Matrix<2, 2, float> res2 = c.dot<int>(d); // [[ 40, 49 ],[ 85, 103 ]]
mu::Matrix<2, 2, float> res3 = c.dot<float>(d); // [[ 41.5,49 ],[ 86.5,103 ]]

Template Parameters

U
N2
M2
T2

Parameters

rhs

Returns: std::conditional_t<std::is_same<U, void>::value, Matrix<N, M2, T>, Matrix<N, M2, U>>

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dot() [2/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = void, std::size_t N2, typename T2 >

std::conditional_t<std::is_same<U, void>::value, Vector<N, T>, Vector<N, U> > mu::Matrix< N, M, T >::dot ( const Vector< N2, T2 > & rhs ) const

inline

dot product of a matrix and a vector

For a Matrix \( A \) of size \( N \times M \) and a Vector \( b \) of size \( M \) the result is a Vector \( c \) of size \( N \),

\( c = A \cdot b \) with

\( c_{j} = A_{j1} b_1 + A_{j2} b_2 + ... + A_{jM} b_M = \sum_{i=1}^{M} A_{ji} b_i \)

Second Matrix dimension (M) must be equal to the size of the Vector (N)

For two objects of the same type, specifying the return type is optional. It will be of the type of the two objects by default.

For two objects of different types, specifying the return type is required.

return value is a Vector of the size of the first Matrix dimension (N) containing the type of the two objects or else of the explicitly stated type

Example: // same types
mu::Matrix<2, 3, int> a{{3, 4, 5}, {6, 7, 8}};
mu::Vector<3, int> b{1, 2, 3};
mu::Vector<2, int> res1 = a.dot(b); // [ 26, 44 ]
// different types (must specify internal precision)
mu::Matrix<2, 3, int> c{{3, 4, 5}, {6, 7, 8}};
mu::Vector<3, float> d{1.5F, 2.5F, 3.5F};
mu::Vector<2, float> res2 = c.dot<int>(d); // [ 31, 54 ]
mu::Vector<2, float> res3 = c.dot<float>(d); // [ 32, 54.5 ]

Template Parameters

U
N2
T2

Parameters

rhs

Returns: std::conditional_t<std::is_same<U, void>::value, Vector<N, T>, Vector<N, U>>

Here is the call graph for this function:

◆ end() [1/2]

template<std::size_t N, std::size_t M, typename T>

iterator mu::Matrix< N, M, T >::end ( )

inlinenoexcept

returns a iterator starting at one after the last row

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
mu::Vector<3, int> last = *(a.end() - 1); // [ 2, 4, 8 ]

Returns: iterator

Here is the caller graph for this function:

◆ end() [2/2]

template<std::size_t N, std::size_t M, typename T>

const_iterator mu::Matrix< N, M, T >::end ( ) const

inlinenoexcept

returns a const iterator starting at one after the last row

Example: const mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
mu::Vector<3, int> last = *(a.end() - 1); // [ 2, 4, 8 ]

Returns: const_iterator

◆ max()

template<std::size_t N, std::size_t M, typename T>

T mu::Matrix< N, M, T >::max ( ) const

inline

get the max value of the matrix

Example: mu::Matrix<2, 3, int> a{{8, 5, 3}, {4, 5, 6}};
int max = a.max(); // 8

Returns: T

Here is the call graph for this function:

Here is the caller graph for this function:

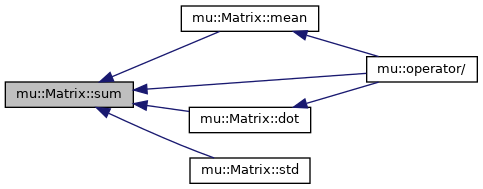
◆ mean()

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

U mu::Matrix< N, M, T >::mean ( ) const

inline

mean of all the elements of the matrix

specifying the return type is optional. It will be of the type of the Vector by default.

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
float mean1 = a.mean(); // 2 (because a holds type int)
float mean2 = a.mean<float>(); // 2.5F

Template Parameters

U

Returns: U

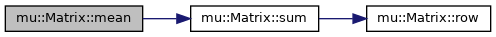
Here is the call graph for this function:

Here is the caller graph for this function:

◆ min()

template<std::size_t N, std::size_t M, typename T>

T mu::Matrix< N, M, T >::min ( ) const

inline

get the min value of the matrix

Example: mu::Matrix<2, 3, int> a{{8, 5, 3}, {4, 5, 6}};
int min = a.min(); // 3

Returns: T

Here is the call graph for this function:

Here is the caller graph for this function:

◆ n_cols()

template<std::size_t N, std::size_t M, typename T>

constexpr size_type mu::Matrix< N, M, T >::n_cols ( ) const

inlinenoexcept

returns the number of columns

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
std::size_t n_cols = a.n_cols(); // 3

Returns: constexpr size_type

◆ n_rows()

template<std::size_t N, std::size_t M, typename T>

constexpr size_type mu::Matrix< N, M, T >::n_rows ( ) const

inlinenoexcept

returns the number of rows

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
std::size_t n_rows = a.n_rows(); // 2

Returns: constexpr size_type

◆ operator!=()

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

bool mu::Matrix< N, M, T >::operator!= ( const Matrix< N, M, U > & rhs ) const

inline

unequality operator

Parameters

rhs

Returns: bool true if unequal, false if equal

Here is the call graph for this function:

◆ operator*=() [1/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

Matrix<N, M, T>& mu::Matrix< N, M, T >::operator*= ( const Matrix< N, M, U > & rhs )

inline

multiplication equal operator

subject to implicit conversions

Template Parameters

U

Parameters

rhs

Returns: Matrix<N, M, T>&

◆ operator*=() [2/2]

template<std::size_t N, std::size_t M, typename T>

template<class TScalar >

std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &> mu::Matrix< N, M, T >::operator*= ( const TScalar & scalar )

inline

multiply a scalar with this matrix

Template Parameters

TScalar

Parameters

scalar

Returns: std::enable_if_t<std::is_arithmetic<TScalar>::value,Matrix<N, M, T> &>

Here is the call graph for this function:

◆ operator+=() [1/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

Matrix<N, M, T>& mu::Matrix< N, M, T >::operator+= ( const Matrix< N, M, U > & rhs )

inline

plus equal operator

subject to implicit conversions

Template Parameters

U

Parameters

rhs

Returns: Matrix<N, M, T>&

◆ operator+=() [2/2]

template<std::size_t N, std::size_t M, typename T>

template<class TScalar >

std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &> mu::Matrix< N, M, T >::operator+= ( const TScalar & scalar )

inline

add a scalar to this matrix

Template Parameters

TScalar

Parameters

scalar

Returns: std::enable_if_t<std::is_arithmetic<TScalar>::value,Matrix<N, M, T> &>

Here is the call graph for this function:

◆ operator-=() [1/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

Matrix<N, M, T>& mu::Matrix< N, M, T >::operator-= ( const Matrix< N, M, U > & rhs )

inline

minus equal operator

subject to implicit conversions

Template Parameters

U

Parameters

rhs

Returns: Matrix<N, M, T>&

◆ operator-=() [2/2]

template<std::size_t N, std::size_t M, typename T>

template<class TScalar >

std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &> mu::Matrix< N, M, T >::operator-= ( const TScalar & scalar )

inline

subtract a scalar from every element of this matrix

Template Parameters

TScalar

Parameters

scalar

Returns: std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &>

Here is the call graph for this function:

◆ operator/=() [1/2]

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

Matrix<N, M, T>& mu::Matrix< N, M, T >::operator/= ( const Matrix< N, M, U > & rhs )

inline

divison equal operator

subject to implicit conversions

Template Parameters

U

Parameters

rhs

Returns: Matrix<N, M, T>&

◆ operator/=() [2/2]

template<std::size_t N, std::size_t M, typename T>

template<class TScalar >

std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &> mu::Matrix< N, M, T >::operator/= ( const TScalar & scalar )

inline

divide every element of this matrix by a scalar

division by zero on integral types triggers an assert

Template Parameters

TScalar

Parameters

scalar

Returns: std::enable_if_t<std::is_arithmetic<TScalar>::value, Matrix<N, M, T> &>

Here is the call graph for this function:

◆ operator=() [1/2]

template<std::size_t N, std::size_t M, typename T>

Matrix& mu::Matrix< N, M, T >::operator= ( const Matrix< N, M, T > & other )

default

Copy assignment operator.

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Matrix<2, 2, int> b = a;

Parameters

other

Returns: Matrix&

Here is the caller graph for this function:

◆ operator=() [2/2]

template<std::size_t N, std::size_t M, typename T>

Matrix& mu::Matrix< N, M, T >::operator= ( Matrix< N, M, T > && other )

defaultnoexcept

Move assignment operator.

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Matrix<2, 2, int> b = std::move(a);

Parameters

other

Returns: Matrix&

◆ operator==()

template<std::size_t N, std::size_t M, typename T>

template<typename U = T>

bool mu::Matrix< N, M, T >::operator== ( const Matrix< N, M, U > & rhs ) const

inline

equality operator

see mu::Vector operator== for more information.

Parameters

rhs

Returns: bool true if equal, false if unequal

Here is the caller graph for this function:

◆ operator[]() [1/2]

template<std::size_t N, std::size_t M, typename T>

Vector<M, T>& mu::Matrix< N, M, T >::operator[] ( size_type idx )

inlinenoexcept

access a row within the matrix

does not throw an exception if idx is out of range

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Vector<2, int> b = a[0]; // [ 1, 2 ]
int a21 = a[1][0]; // 3

Parameters

idx

Returns: T&

◆ operator[]() [2/2]

template<std::size_t N, std::size_t M, typename T>

const Vector<M, T>& mu::Matrix< N, M, T >::operator[] ( size_type idx ) const

inlinenoexcept

const access a row within the matrix

does not throw an exception if idx is out of range

Example: const mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
mu::Vector<2, int> b = a[0]; // [ 1, 2 ]
int a21 = a[1][0]; // 3

Parameters

idx

Returns: const T&

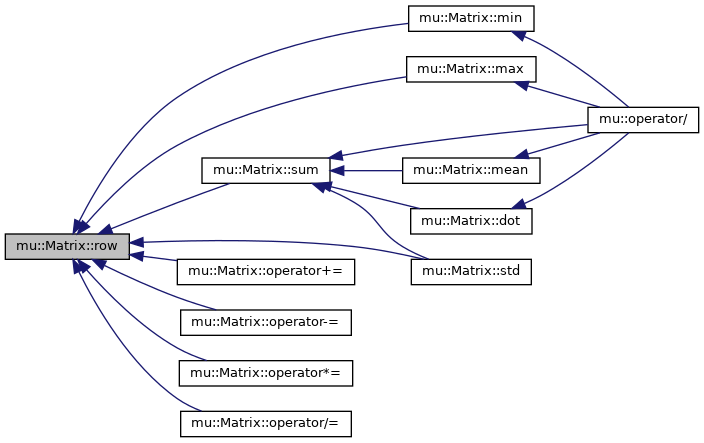
◆ row()

template<std::size_t N, std::size_t M, typename T>

Vector<M, T> mu::Matrix< N, M, T >::row ( const size_type & idx ) const

inline

get a matrix row as a vector

an invalid index that exceeds the matrix dimension causes a runtime error

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
mu::Vector<3, int> first_row = a.row(0); // [ 1, 2, 4 ]

Parameters

idx

Returns: Vector<M, T>

Here is the caller graph for this function:

◆ size()

template<std::size_t N, std::size_t M, typename T>

constexpr std::array<size_type, 2> mu::Matrix< N, M, T >::size ( ) const

inlinenoexcept

returns the matrix dimensions as an array of size 2

[0] rows
[1] columns

Example: mu::Matrix<2, 3, int> a{{1, 2, 4}, {2, 4, 8}};
std::size_t n_rows = a.size()[0]; // 2
std::size_t n_cols = a.size()[1]; // 3

Returns: constexpr std::array<size_type, 2>

◆ std()

template<std::size_t N, std::size_t M, typename T>

template<class U = T>

U mu::Matrix< N, M, T >::std ( ) const

inline

calculates the standard deviation

\( \sigma = \sqrt{\frac{\sum(x_ij - \mu)^2}{N}} \)

Example: mu::Matrix<2, 2, int> a{{2, 3}, {5, 7}};
float std1 = a.std(); // 1 (because a holds type int)
float std2 = a.std<float>(); // 1.92028642

Template Parameters

U

Returns: U

Here is the call graph for this function:

◆ sum()

template<std::size_t N, std::size_t M, typename T>

T mu::Matrix< N, M, T >::sum ( ) const

inline

sum up all the elements of the matrix

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
int sum = a.sum(); // 10

Returns: T

Here is the call graph for this function:

Here is the caller graph for this function:

◆ transpose()

template<std::size_t N, std::size_t M, typename T>

void mu::Matrix< N, M, T >::transpose ( )

inline

transposes this Matrix object

only works for symmetrical matrices!!!

Example: mu::Matrix<2, 2, int> a{{1, 2}, {3, 4}};
a.transpose();

Here is the caller graph for this function:

◆ transposed()

template<std::size_t N, std::size_t M, typename T>

Matrix<M, N, T> mu::Matrix< N, M, T >::transposed ( ) const

inline

creates and returns a transposed Matrix object

Example: mu::Matrix<2, 3, int> a{{1, 2, 3}, {4, 5, 6}};
mu::Matrix<3, 2, int> a_transposed = a.transposed();

Returns: Matrix<M, N, T>

Here is the caller graph for this function:

Friends And Related Function Documentation

◆ operator<<

template<std::size_t N, std::size_t M, typename T>

template<std::size_t Nn, std::size_t Mm, class U >

std::ostream& operator<<	(	std::ostream &	os,
		const Matrix< Nn, Mm, U > &	m
	)

friend

print matrix values

forwards Vector for every row

Example: mu::Matrix<2, 2, int> a{{2, 3}, {5, 7}};
// std::cout << a << std::endl;
// [ [ 2, 3 ],
// [ 5, 7 ] ]

Template Parameters

Nn
U

Parameters

os
v

Returns: std::ostream&

The documentation for this class was generated from the following file:

/home/runner/work/mu/mu/include/mu/matrix.h

Public Types

Public Member Functions

Protected Attributes

Friends

Detailed Description

template<std::size_t N, std::size_t M, typename T> class mu::Matrix< N, M, T >

Constructor & Destructor Documentation

◆ Matrix() [1/9]

◆ Matrix() [2/9]

◆ Matrix() [3/9]

◆ Matrix() [4/9]

◆ Matrix() [5/9]

◆ Matrix() [6/9]

◆ Matrix() [7/9]

◆ Matrix() [8/9]

◆ Matrix() [9/9]

Member Function Documentation

◆ at() [1/2]

◆ at() [2/2]

◆ begin() [1/2]

◆ begin() [2/2]

◆ col()

◆ det()

◆ diag()

◆ dot() [1/2]

◆ dot() [2/2]

◆ end() [1/2]

◆ end() [2/2]

◆ max()

◆ mean()

◆ min()

◆ n_cols()

◆ n_rows()

◆ operator!=()

◆ operator*=() [1/2]

◆ operator*=() [2/2]

◆ operator+=() [1/2]

◆ operator+=() [2/2]

◆ operator-=() [1/2]

◆ operator-=() [2/2]

◆ operator/=() [1/2]

◆ operator/=() [2/2]

◆ operator=() [1/2]

◆ operator=() [2/2]

◆ operator==()

◆ operator[]() [1/2]

◆ operator[]() [2/2]

◆ row()

◆ size()

◆ std()

◆ sum()

◆ transpose()

◆ transposed()

Friends And Related Function Documentation

◆ operator<<

template<std::size_t N, std::size_t M, typename T>
class mu::Matrix< N, M, T >